[
Click here for a PDF of this post with nicer formatting]
The Setup
(a) Large horizontal scale

(b) ``Zoomed in''
Figure 1: The Heaviside step function. Note how it doesn't matter how close we get to
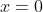
the function looks exactly the same.
The Heaviside step function
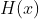
, sometimes called the Heaviside theta function, appears in many places in physics, see [1] for a brief discussion. Simply put, it is a function whose value is zero for
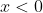
and one for
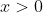
. Explicitly,
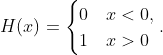
(1)
We won't worry about precisely what its value is at zero for now, since it won't effect our discussion, see [2] for a lengthier discussion. Fig. 1 plots
. The key point is that crossing zero flips the function from 0 to 1.
Derivative -- The Dirac Delta Function
(a) Dirac delta function

(b) Ramp function
Figure 2: The derivative (a), and the integral (b) of the Heaviside step function.
Say we wanted to take the derivative of
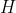
. Recall that a derivative is the slope of the curve at at point. One way of formulating this is
(2)
Now, for any points
or
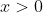
, graphically, the derivative is very clear:
is a flat line in those regions, and the slope of a flat line is zero. In terms of (2),
does not change, so
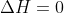
and
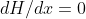
. But if we pick two points, equally spaced on opposite sides of
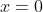
, say
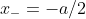
and
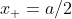
, then
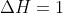
and
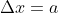
. It doesn't matter how small we make

,
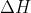
stays the same. Thus, the fraction in (2) is
(3)
Graphically, again, this is very clear:
 jumps
jumps from 0 to 1 at zero, so it's slope is essentially vertical, i.e. infinite. So basically, we have
(4)
This function is, loosely speaking, a ``Dirac Delta'' function, usually written as
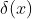
, which has seemingly endless uses in physics.
We'll note a few properties of the delta function that we can derive from (4). First, integrating it from
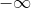
to any
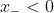
:
(5)
since
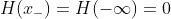
. On the other hand, integrating the delta function to any point greater than
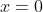
:
(6)
since
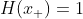
.
At this point, I should point out that although the delta function blows up to infinity at
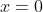
, it still has a finite integral. An easy way of seeing how this is possible is shown in Fig. 2(a). If the width of the box is
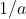
and the height is

, the area of the box (i.e. its integral) is
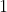
, no matter how large

is. By letting

go to infinity we have a box with infinite height, yet, when integrated, has finite area.
Integral -- The Ramp FunctionNow that we know about the derivative, it's time to evaluate the integral. I have two methods of doing this. The most straightforward way, which I first saw from Prof. T.H. Boyer, is to integrate
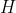
piece by piece. The integral of a function is the area under the curve,
1 and when
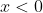
there is no area, so the integral from
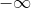
to any point less than zero is zero. On the right side, the integral to a point
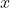
is the area of a rectangle of height 1 and length
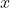
, see Fig. 1(a). So, we have
(7)
We'll call this function a ``ramp function,''
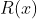
. We can actually make use of the definition of
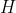
and simplify the notation:
(8)
since
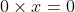
and
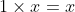
. See Fig. 2(b) for a graph -- and the reason for calling this a ``ramp'' function.
But I have another way of doing this which makes use of a trick that's often used by physicists:
We can always add zero for free, since
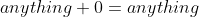
. Often we do this by adding and subtracting the same thing,
(9)
for example. But we can use the delta function (4) to add zero in the form
(10)
Since
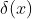
is zero for
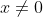
, the
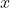
part doesn't do anything in those regions and this expression is zero. And, although
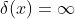
at
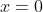
,
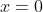
at
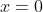
, so the expression is still zero.
So we'll add this on to
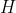
:
(11)
where the last step follows from the ``product rule'' for differentiation. At this point, to take the integral of a full differential is trivial, and we get (8).
References[1] M. Springer. Sunday function [online]. February 2009. Available from:
http://scienceblogs.com/builtonfacts/2009/02/sunday_function_22.php [cited 30 June 2009].
[2] E.W. Weisstein. Heaviside step function [online]. Available from:
http://mathworld.wolfram.com/HeavisideStepFunction.html [cited 30 June 2009].
1 To be completely precise, it's the (signed) area between the curve and the line
.
 (a) Large horizontal scale
(a) Large horizontal scale (b) ``Zoomed in''
(b) ``Zoomed in'' (a) Dirac delta function
(a) Dirac delta function (b) Ramp function
(b) Ramp function


