Behind the Guesses: July 2009

[Click here for a PDF of this post with nicer formatting]
The Setup

Figure 1: An example of a section cylindrical waveguide with embedded coordinate axes.

A conducting waveguide is a metal tube -- think pipe or air conditioning duct, for example -- through which electromagnetic waves can propagate. If you want to know what real-life waveguides look like, just do a quick internet image search. We'll assume the length of the tube is oriented along the $z$ -direction, see Fig 1. There is no loss of generality in doing this, since we can always choose a coordinate system as we like. So really, we're picking a coordinate system such that the $z$ -axis points along the tube.

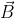
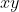
Now, we can decompose the electric field $\vec{E}$ and magnetic (inductance) field $\vec{B}$ vectors into two parts each. One part points along the $z$ (normal) direction while the other is pointing somewhere in the $xy$ (transverse) plane. Explicitly:

$\vec{E}= E_z\hat{z} +\vec{E}_t$

(1a)

$\vec{B}= B_z\hat{z} +\vec{B}_t$

(1b)

In the first([1], Eq. (8.24)) and third[2], Eq. (8.26)) editions of Classical Electrodynamics, J.D. Jackson gives the transverse fields in terms of the $z$ -components of the fields. (I have no idea why he left the complete expression out of the second edition.) In the third edition, for example, he assumes plane wave propagation in the positive $z$ direction -- that is an $e^{+ikz}$ dependance -- and simply states, without any real explanation:

the transverse fields are
$\vec{E}_t=\frac{i}{\left(\mu\epsilon\frac{\omega^2}{c^2}-k^2\right)}\left[k\nabla_tE_z-\frac{\omega}{c}\hat{z} \times\nabla_t B_z\right]$
$\vec{B}_t=\frac{i}{\left(\mu\epsilon\frac{\omega^2}{c^2}-k^2\right)}\left[k\nabla_tB_z+\mu\epsilon\frac{\omega}{c}\hat{z} \times\nabla_t E_z\right]$

where I've converted his new choice of MKSA units back into the clearer CGS units. However, back in the first edition he does not insist on the assumption of positive $z$ propagation. Moreover, he does not just state the fields; he suggests a method for getting them -- namely, manipulation of the curl equations in Maxwell's equations. However, in that edition, he does not expand the curl equations in light of the separation of the fields into transverse and parallel components as he does in the second and third editions.

Because of all this confusion, I'm going to derive the cavity modes fully, starting from Maxwell's equations, once and for all. This derivation is based on a combination of all three editions of Jackson's book. This is a tedious, although not completely trivial exercise. Brace yourselves for quite a bit of algebra.

Maxwell's Equations - The Curls
Here we'll deal with the two curl equations in Maxwell's equations:

$\nabla\times\vec{E}=-\frac{1}{c}\frac{\partial\vec{B}}{\partial t}$

(2a)

$\nabla\times\vec{H}=\frac{1}{c}\frac{\partial\vec{D}}{\partial t}+\frac{4\pi}{c}\vec{J}$

(2b)

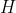
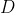
where $H$ is the magnetic field and $D$ is the electric displacement field. We will assume the inside of the waveguide has uniform permittivity and permeability, so $\vec{D}=\epsilon\vec{E}$ and $\vec{B}=\mu \vec{H}$ . Also, we'll assume the absence of any currents, so $\vec{J}=0$ and we'll drop it from here on. Additionally, we'll assume the same sinusoidal time dependance $e^{-i\omega t}$ for both the fields. Thus, the time derivatives ``bring down'' a factor of $-i\omega$ .

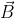
Furthermore, since we're splitting up $\vec{E}$ and $\vec{B}$ into normal and transverse parts, we'll do the same with the gradient operator $\nabla$ :

$\nabla=\underbrace{\hat{x}\frac{\partial }{\partial x}+\hat{y}\frac{\partial }{\partial y}}_{\equiv\nabla_t}+\hat{z} \frac{\partial }{\partial z}=\nabla_t+\hat{z} \frac{\partial }{\partial z}$

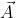
Because curl equations are annoying, and because we're ultimately looking for an equation for the transverse fields, I'm going to try and get rid of the $\nabla\times$ 's. The symmetry of form in (2) means that we'll only need to do these calculations once; I will use $\vec{A}$ in place of either $\vec E$ or $\vec B$ .
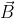
First, we'll expand $\nabla\times\vec{A}$ :

$\nabla\times\vec{A} = \left[\nabla_t+\hat{z} \frac{\partial}{\partial z}\right]\time\left[\vec{A}_t+\hat{z} A_z\right]$

$=\nabla_t\times\at+\nabla_t\times\hat{z} A_z+\frac{\partial}{\partial z}\left[\hat{z} \times\at\right]+\frac{\partial}{\partial z}\left[\cancel{\hat{z} \times\hat{z} }^{\,0}A_z\right]$

(3)

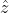
We've killed one term through this expansion. However, the leftmost cross product term $\nabla_t\times\vec{A}_t$ gives a quantity with only a $z$ component. The righthand side of these equations also have a $\hat{z}$ term. We can get rid of both by multiplying the entire equation(s) by $\hat{z} \times$ :

$\hat{z} \times\nabla\times\vec{A} = \cancel{\hat{z}\times\nabla_t\times\vec{A}_t}^{\,0}+\hat{z}\times\nabla_t\times\hat{z} A_z+\frac{\partial }{\partial z}\left[\underbrace{\hat{z} \times\hat{z}\times\vec{A}_t}_{-\vec{A}_t}\right]$

$= \hat{z} \times\nabla_t\times\hat{z} A_z-\frac{\partial \vec{A}_t}{\partial z}$

(4)

Figure 2: Vectors $\vec{A}_t$ , $\hat{z} \times\vec{A}_t$ and $\hat{z} \times\hat{z} \times\vec{A}_t$ .

For why $\hat{z} \times\hat{z} \times\vec{A}_t=-\vec{A}_t$ see Fig. 2. Also, we note that

$\hat{z} \times\nabla_t\times\hat{z} =\hat{z} \times(-\hat{z}\times\nabla_t)=\nabla_t$

(5)

for the same reason. We could have used the vector multiplication identity

$a\times (b\times c)=(a\cdot c)b-(a\cdot b)c$

to simplify both of these expressions, or expanded $\nabla_t$ and $\vec{A}_t$ and carried through even more algebra, but I think the picture is clearer.

Thus,

$\hat{z} \times\nabla\times\vec{A} =\nabla_t A_z-\frac{\partial\vec{A}_t}{\partial z},$

(6)

and we can write (2) as

$\nabla_t E_z-\frac{\partial \vec{E}_t}{\partial z}&=\frac{i\omega}{c}\hat{z} \times\vec{B}_t$

(7a)

$\nabla_t B_z-\frac{\partial \vec{B}_t}{\partial z}&=-i\mu\epsilon\frac{\omega}{c}\hat{z} \times\vec{E}_t$

(7b)

At this point, it's time to introduce the explicit $z$ dependence and process the $z$ derivatives.

Some $\pm$ and $\mp$ notes
Unlike Jackson, who works with the assumption of upward propagating waves -- i.e. an $e^{+ikz}$ dependence -- we'll work with an assumed $e^{\pm i k z}$ dependance, thus allowing both upward and downward propagating waves. Thus, the $z$ derivatives ``bring down'' a factor of $\pm ik$ . Whenever we have $\pm$ or $\mp$ the upper symbol is the sign for upward propagating waves, the lower symbol is for downward propagating. Because we'll be mucking about with these plus-minus guys in some algebra, I want to get a few issues out of the way.

The first thing to keep in mind about these plus-minus operators is that an equation like

$A = \pm C + D$

(8)

is shorthand for two different equations:

$A = +C+D$

(9a)

$A = -C+D$

(9b)

So, there are essentially two ways to approach these things. One way is to carefully trace at the outset what happens to $\pm$ or $\mp$ under various arithmetic operations like addition, multiplication, etc. This has the benefit of being more concise -- you only need to write each equation once -- but is a lot easier to make errors and hides the double-equation nature of the symbol. I'll admit, though, that when I'm writing a paper I'm generally inclined to take this path.

However, for the purposes of this blog post, I'll explicitly carry out the calculations in parallel equations. (This really looks much better in the PDF. If anyone has any suggestions for improving the web version, please, let me know!) The left-hand column corresponds to $+$ , the right-hand column to $-$ . At the end I will also show what the results looks like in the shorthand notation and I encourage you to work out the rules on your own. Perhaps in another post I'll address the shorthand notation in detail.

Some more algebra
Now, it's time for some more algebra.¹ Taking the $z$ derivative in (7) gives:

$\nabla_t E_z-i k\vec{E}_t=i\frac{\omega}{c}\hat{z}\times\vec{B}_t$

$\nabla_t E_z+ i k\vec{E}_t=i\frac{\omega}{c}\hat{z}\times\vec{B}_t$

(10)

and

$\nabla_t B_z-i k\vec{B}_t= -i\mu\epsilon\frac{\omega}{c}\hat{z}\times\vec{E}_t$

$\nabla_t B_z+i k\vec{B}_t= -i\mu\epsilon\frac{\omega}{c}\hat{z}\times\vec{E}_t$

(11)

Solving (10) for $\vec{E}_t$ gives

$\vec{E}_t=- \frac{i}{k}\nabla_tE_z-\frac{\omega}{ck}\hat{z}\times\vec{B}_t$

$\vec{E}_t=+ \frac{i}{k}\nabla_tE_z+\frac{\omega}{ck}\hat{z}\times\vec{B}_t$

(12)

Substituting this into (11) and simplifying:

$\nabla_t B_z-i k\vec{B}_t=-i\mu\epsilon\frac{\omega}{c}\hat{z} \times\left[-\frac{i}{k}\nabla_tE_z-\frac{\omega}{ck}\hat{z}\times\vec{B}_t\right]$	\|	$\nabla_t B_z+i k\vec{B}_t=-i\mu\epsilon\frac{\omega}{c}\hat{z}\times\left[\frac{i}{k}\nabla_tE_z+\frac{\omega}{ck}\hat{z}\times\vec{B}_t \right]$
$=-\frac{\mu\epsilon}{k}\frac{\omega}{c}\hat{z}\times\nabla_tE_z +i\frac{\mu\epsilon}{k}\frac{\omega^2}{c^2}\underbrace{\hat{z}\times\hat{z} \times\vec{B}_t}_{-\vec{B}_t}$	\|	$=\frac{\mu\epsilon}{k}\frac{\omega}{c}\hat{z}\times\nabla_tE_z -i\frac{\mu\epsilon}{k}\frac{\omega^2}{c^2}\underbrace{\hat{z}\times\hat{z} \times\vec{B}_t}_{-\vec{B}_t}$
$\nabla_tB_z=-\frac{i}{k}\left(\mu\epsilon\frac{\omega^2}{c^2}- k^2\right)\vec{B}_t - \frac{\mu\epsilon}{k}\frac{\omega}{c}\hat{z}\times\nabla_tE_z$	\|	$\nabla_tB_z=+\frac{i}{k}\left(\mu\epsilon\frac{\omega^2}{c^2}-k^2\right)\vec{B}_t+\frac{\mu\epsilon}{k}\frac{\omega}{c}\hat{z} \times\nabla_tE_z$

(13)

Solving this for $\vec{B}_t$ gives:

$\vec{B}_t = \frac{1}{\left(\mu\epsilon\frac{\omega^2}{c^2}- k^2\right)}\left[ ik\nabla_t B_z +i\mu\epsilon\frac{\omega}{c}\hat{z} \times\nabla_tE_z\right]$

$\vec{B}_t = \frac{1}{\left(\mu\epsilon\frac{\omega^2}{c^2}- k^2\right)}\left[ -ik\nabla_t B_z +i\mu\epsilon\frac{\omega}{c}\hat{z} \times\nabla_tE_z\right]$

(14)

Or, in $\pm$ form:

$\boxed{\vec{B}_t = \frac{1}{\left(\mu\epsilon\frac{\omega^2}{c^2}- k^2 \right)}\left[ \pm ik\nabla_t B_z +i\mu\epsilon\frac{\omega}{c}\hat{z} \times\nabla_tE_z\right]}$

(15)

In the first edition, Jackson converts the $\pm ik B_z$ back into $\frac{\partial B_z}{\partial z}$ to get rid of the $\pm$ , but I feel this confuses things, as this expression only holds for a plane wave in the $z$ direction. In any case, we now substitute this expression for $\vec{B}_t$ back into (12) and simplify:

$\vec{E}_t=- \frac{i}{k}\nabla_tE_z-\frac{\omega}{ck}\hat{z}\times\frac{1}{\left(\mu\epsilon\frac{\omega^2}{c^2}- k^2\right)}\left[ ik\nabla_t B_z +i\mu\epsilon\frac{\omega}{c}\hat{z} \times\nabla_tE_z\right]$	\|	$\vec{E}_t= \frac{i}{k}\nabla_tE_z+\frac{\omega}{ck}\hat{z} \times\frac{1}{\left(\mu\epsilon\frac{\omega^2}{c^2}- k^2 \right)}\left[-ik\nabla_t B_z + i\mu\epsilon\frac{\omega}{c}\hat{z}\times\nabla_tE_z\right]$
$=- \frac{i}{k}\nabla_tE_z- \left[i\frac{\omega}{c}\frac{1}{\left(\mu\epsilon\frac{\omega^2}{c^2}-k^2 \right)}\hat{z} \times\nabla_t B_z + \frac{i}{k}\frac{\mu\epsilon\frac{\omega^2}{c^2}}{\left(\mu\epsilon\frac{\omega^2}{c^2}-k^2 \right)}\underbrace{\hat{z} \times\hat{z}\times\nabla_tE_z}_{-\nabla_tE_z}\right]$	\|	$= \frac{i}{k}\nabla_tE_z + \left[-i\frac{\omega}{c}\frac{1}{\left(\mu\epsilon\frac{\omega^2}{c^2}-k^2 \right)}\hat{z} \times\nabla_t B_z + \frac{i}{k}\frac{\mu\epsilon\frac{\omega^2}{c^2}}{\left(\mu\epsilon\frac{\omega^2}{c^2}-k^2\right)} \underbrace{\hat{z} \times\hat{z}\times\nabla_tE_z}_{-\nabla_tE_z}\right]$
$=ik\frac{1}{\left(\mu\epsilon\frac{\omega^2}{c^2}-k^2 \right)}\nabla_tE_z-i\frac{\omega}{c}\frac{1}{\left(\mu\epsilon\frac{\omega^2}{c^2}-k^2 \right)}\hat{z} \times \nabla_t B_z$	\|	$=-ik\frac{1}{\left(\mu\epsilon\frac{\omega^2}{c^2}-k^2 \right)}\nabla_tE_z-i\frac{\omega}{c}\frac{1}{\left(\mu\epsilon\frac{\omega^2}{c^2}-k^2 \right)}\hat{z} \times \nabla_t B_z$
$=\frac{1}{\left(\mu\epsilon\frac{\omega^2}{c^2}- k^2\right)}\left[ik\nabla_tE_z -i\frac{\omega}{c}\hat{z} \times\nabla_t B_z\right]$	\|	$=\frac{1}{\left(\mu\epsilon\frac{\omega^2}{c^2}- k^2\right)}\left[-ik\nabla_tE_z -i\frac{\omega}{c}\hat{z} \times\nabla_t B_z\right]$

(16)

Or, in $\pm$ form:

$\boxed{\vec{E}_t=\frac{1}{\left(\mu\epsilon\frac{\omega^2}{c^2}-k^2\right)}\left[\pm ik\nabla_t E_z-i\frac{\omega}{c}\hat{z} \times\nabla_t B_z\right]}$

(17)

So, we've finally achieved Jackson's result, allowing for both upward and downward propagating waves.

References
[1] J.D. Jackson. Classical Electrodynamics. John Wiley & Sons, Inc., 1st edition, 1966.
[2] J.D. Jackson. Classical Electrodynamics. John Wiley & Sons, Inc., 3rd edition, 1998.

¹ In case you were wondering why Jackson left out the whole calculation...