The Quantum Harmonic Oscillator Ladder Operators

[Click here for a PDF of this post with nicer formatting]

The Setup

As a first example, I'll discuss a particular pet-peeve of mine, which is something covered in many introductory quantum mechanics classes: The algebraic solution to quantum (1D) simple harmonic oscillator.¹ The one-dimensional, time-independent Schrödinger equation is:

(1)

where 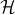is the Hamiltonian of the system. Explicitly, this Hamiltonian is

(2)

where 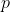is the particle's momentum, 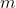is it's mass and is the potential the particle is placed into. The potential associated with a classical harmonic oscillator is

(3)

where . For the sake of convenience, so we don't get bogged down with various factors,² we'll consider . Then, if we substitute (3) back into (2) we write the Hamiltonian as:

(4)

A bad way

Figure 1: How Einstein developed his famous expression.

Now, at this point, many texts, (see [1] or [2] for example,) define, with no motivation other than future ``convenience'', two operators

(5a)

(5b)

and proceed to show how these can be used to simplify the Hamiltonian and easily solve the problem. While it is an elegant and quick solution, this presentation is completely useless. I find it highly unlikely that Dirac sat down to solve this problem and tried a whole series of random operators

and so on, along with their complex conjugates, until he lucked out with the solution in (5), see Fig. 1.

A better way

What is far more likely is the argument given by Griffiths in [3], which I'll loosely follow. He presents a rationale and a method for approaching this problem. Namely, he suggests factoring the Hamiltonian (4) into terms linear in 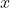and 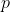. If we ignore the operator properties of 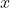and 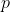momentarily, and consider the classical quantities, we can factor the Hamiltonian

(6)

Now we see a reason why (5) makes sense to try. Each term, either on the right or left side of (6),³ contains two terms which are complex conjugates of each other. If this were a classical problem, we could, in principle, make a change of variables converting the Hamiltonian to something of the form

(7)

where is any of the combinations of 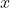and 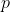in (6). Although this is not a ``canonical transformation,'' the symmetric form⁴ of the Hamiltonian allows us to reduce the Hamiltonian from a function of two dynamical variables to a function of a single dynamical variable.

Switching back to quantum mechanics, we now see a rationale for choosing and as we did.⁵ Although deciding which variable to attach the to and its choice of sign is a guess,⁶ we now have a general method for approaching Hamiltonians that look like they might be easily factored classically -- try using the classical factorizations with quantum quantities and see what happens.


References
[1] J.J. Sakurai. Modern Quantum Mechanics. Addison-Wesley, San Francisco, CA, revised edition, 1993.
[2] F. Schwabl. Quantum Mechanics. Springer, 3rd edition, 2005.
[3] D.J. Griffiths. Introduction to Electrodynamics. Pearson Prentice Hall, 3rd edition, 1999.
[4] P.A.M. Dirac. The Principles of Quantum Mechanics. Oxford University Press, USA.

---

¹ I'll be discussing this in the boring algebraic sense of symbols and whatnot, leaving off the geometric/visual interpretation of the algebra for another time.
² Or maybe I'm just lazy
³ And, since this is a classical problem, the order does not matter, either.
⁴ Yes, it's only up to a constant which I've set to one, but you can still symmetrize things by changing to unitless variables, see [2].
⁵ Recall that the for a quantum-mechanical operator/matrix serves the role of the in (7).
⁶ It actually does not matter to the solution of the problem. The only change is which operator acts to `step up' the state. Dirac actually defined his operators with the attached to the variable, see [4].